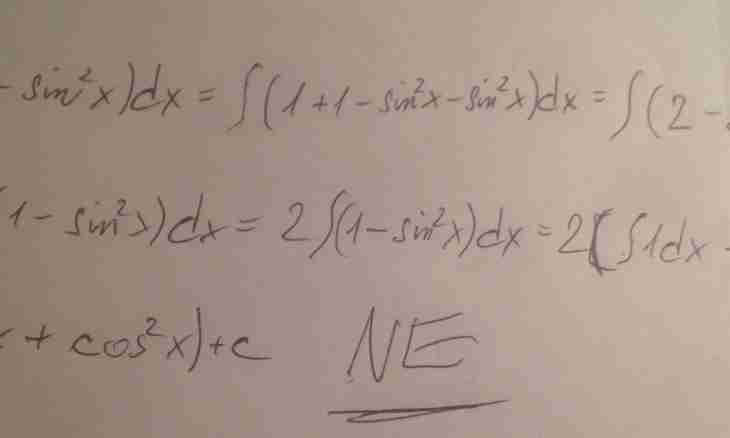Classical models of approximate calculation of a certain integral are based but creation of the integrated sums. These sums have to be the shortest, but providing rather small error of calculation. What for? Since there were serious COMPUTERS and good personal computers, the relevance of a problem of reduction of number of computing operations receded into the background a little. Certainly, without grounds it is not necessary to reject them, and to here weigh between simplicity of an algorithm (where many computing operations) and - will obviously not interfere with complexity of more exact.
Instruction
1. Let's consider a problem of calculation of certain integrals by Monte Carlo method. Application became possible after emergence of the first COMPUTERS therefore Americans Neumann and Ulam are considered as his fathers (from here and the bright name as for those times the best random number generator was the game roulette). From copyright (in the name) I have no right to depart, but now mention either statistical tests, or statistical modeling.
2. For receiving the random numbers possessing the set distribution on an interval (a, b) are used random numbers z, uniform on (0, 1). In the environment of Pascal it corresponds to the subprogramme of Random. On calculators on this case there is a RND button. There are also tables of such random numbers. Stages of modeling of the simplest distributions are also simple (literally excessively). So, an order of calculation of numerical model accidental on (a, b) sizes, which density of probability W(x) following. Having defined function of distribution F(x), equate its zi. Then xi=F^(-1) (zi) (inverse function means). Further receive as is wished much (within opportunities of your personal computer) values of the digital xi model.
3. Now the direct stage of calculations follows. Let you need to calculate a certain integral (see fig. 1a). In figure 1 W (x) it is possible to consider any density of probability of the random variable (RV) distributed on (a, b), and required integral – the expected value of function of this of RV. So the only requirement to the requirement to W(x) – a condition of a normalization (fig. 1b). In mathematical statistics assessment of expected value is the arithmetic average of observed values of the SV function (fig. 1 c). Instead of observations gather their digital models and calculate certain integrals with almost with any desirable accuracy without everyones (sometimes the hardest if to attract Chebyshev's method) calculations.
4. Auxiliary W(x) should be taken the elementary, but, after all, at least slightly reminding (according to the schedule) the integrated function. It is not possible to hide that decrease in an error by 10 times is worth of increase in sample of model by 100 times. So what? When did someone need more than three signs behind a comma? And it is only one million computing operations.