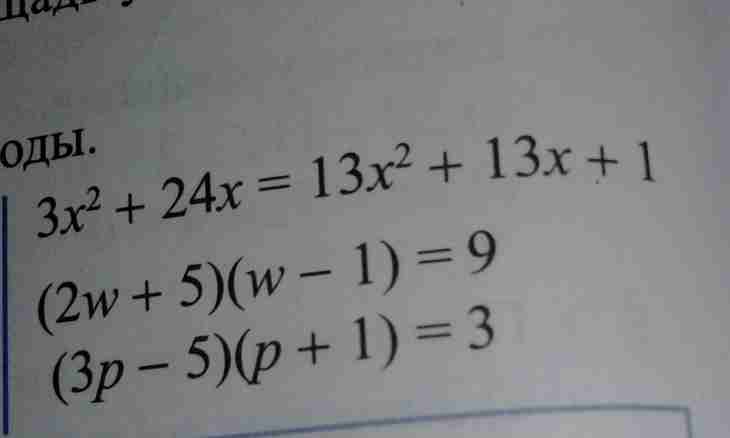For the solution of a quadratic equation it is necessary to find a discriminant of this equation for a start. Having defined a discriminant, it is possible to draw a conclusion on quantity of roots of a quadratic equation at once. Generally for the solution of a polynomial of any order is higher than the second it is also necessary to look for a discriminant.
It is required to you
- knowledge of the simplest mathematical operations
Instruction
1. Let we led a quadratic equation to a type of a(x*x) +b*x+c = 0. Its discriminant will be designated by letter D and will be equal to D = (b*b)-4ac.
2. The discriminant squareof equations can be more than zero. Then the equation has two material roots. If the discriminant is equal to zero, then the equation has one material root. If the discriminant is less than zero, then the equation has no material roots, and has two complex roots. Roots of a quadratic equation will be on formulas: x1 = (-b+sqrt(D)) / 2a, x2 = (-b-sqrt(D)) / 2a (in case of material roots).
3. If a quadratic equation it is possible to present in the form a(x*x) +2*b*x+c = 0, then it is simpler to find the reduced discriminant of this equation in a look: D = (b*b) - ac. With such discriminant the roots of the equation will look as follows: x1 = (-b+sqrt(D)) / a, x2 = (-b-sqrt(D)) / a.