In spite of the fact that the word "perimeter" is translated from Greek as "circle", designate by it the total length of all borders not only a circle, but also any convex geometrical figure. One of such flat figures is the triangle. For finding of length of its perimeter it is necessary to know or lengths of three parties, or to use ratios between lengths of the parties and corners in tops of this figure.
Instruction
1. If lengths of all three parties triangle are known (And, In and C), then for finding of length of perimeter (P) just put them: P = And + In + Page.
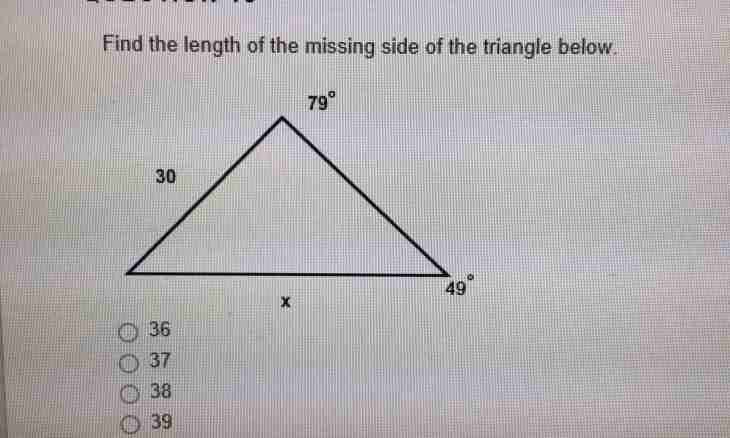
2. If sizes of two corners (α and γ) in tops of any triangle and also length at least of one its party (C), then these data are enough for calculation of lengths of the missing parties are known and consequently also perimeter (P) of a triangle. If the party of the known length lies between corners α and γ, then use the theorem of sine - length of one of the unknown parties can be expressed as sin(α) ∗ With / (sin (180 °-α-γ)), and length another - as sin(γ) ∗ With / (sin (180 °-α-γ)). For calculation of perimeter put these formulas and add to them length of the known party: P = With + sin(α) ∗ With / (sin (180 °-α-γ)) + sin(γ) ∗ With / (sin (180 °-α-γ)).
3. If the party which length is known (C) adjoins only to one of two known corners (α and γ) in a triangle, formulas of calculation of lengths of the missing parties will be a little others. Length of that from them which lies opposite to the only unknown corner can be determined on a formula sin (180 °-α-γ) ∗ In / sin(γ). For calculation of the third party of a triangle use a formula sin(α) ∗ In / sin(γ). For calculation of length of perimeter (P) put both formulas with length of the known party: P = In + sin (180 °-α-γ) ∗ In / sin(γ) + sin(α) ∗ In / sin(γ).
4. If length of only one of the parties, and except lengths of two others is unknown (And yes C) the size of one of corners is given (γ), use the theorem of cosines for calculation of length of the missing party - it will be equal √ (And² + In²-2∗А∗В∗cos(γ)). And for finding of length of perimeter add this expression to lengths of other parties: P = And + In + √ (And² + In²-2∗А∗В∗cos(γ)).
5. If the triangle - rectangular, and the missing party is its leg, then the formula from the previous step can be simplified. For this purpose use Pythagorean theorem from which follows that length of a hypotenuse is equal to a square root from the sum of squares of the known lengths of legs √ (And² + In²). Add to this expression of length of legs for calculation of perimeter: P = And + In + √ (And² + In²).