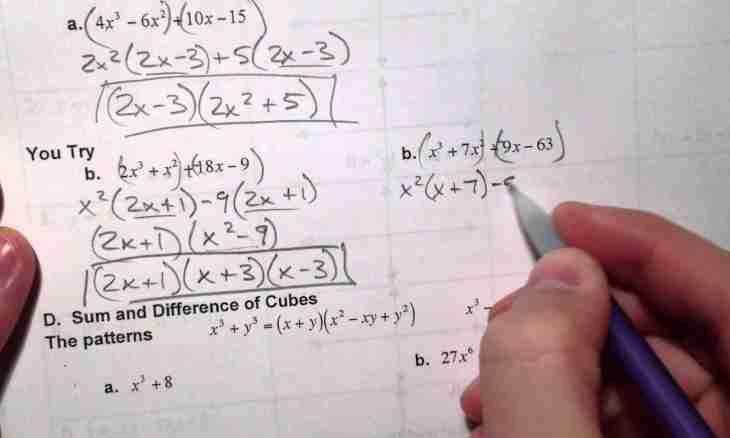Having mastered methods of finding of the decision in case of work with quadratic equations, school students face need to rise by higher degree. However this transition not always seems to lungs, and the requirement to find roots in the equation of the fourth degree sometimes becomes an impossible task.
Instruction
1. Apply Viete's formula which establishes the relations between equation roots in the fourth degree and its coefficients. According to its provisions, the sum of roots gives the size equal to the attitude of the first coefficient towards the second taken with the opposite sign. The order of numbering coincides with decrease of degrees: to the first there corresponds the maximum degree, to the fourth – minimum. The sum of paired works of roots is the attitude of the third coefficient towards the first. Respectively, the sum made of works h1kh2kh3, h1kh3kh4, h1kh2kh4, h2kh3kh4 – the size equal to opposite result of division of the fourth coefficient on the first. And having multiplied all four roots, you receive the number equal to the relation of the free member of the equation to the coefficient facing a variable in the maximum degree. Four equations which are worked out thus give you a system with four unknown for which solution enough basic skills.
2. Check whether your expression belongs to one of types of the equations of the fourth degree which are called ""easily solvable"": biquadratic or returnable. Turn the first into a quadratic equation, having made replacement of parameters and having designated the squared unknown through other variable.
3. Use a standard algorithm of the solution of the returnable equations of the fourth degree in which the coefficients standing on symmetric positions coincide. For the first step divide both members of equation into a square of a required unknown variable. Transform the received expression so that it was possible to make the replacement of a variable turning the initial equation into square. For this purpose in your equation have to remain three composed, two of which contain expressions from the unknown: the first – the sum of its square and reciprocal value, the second – the sum of a variable and its reciprocal value.