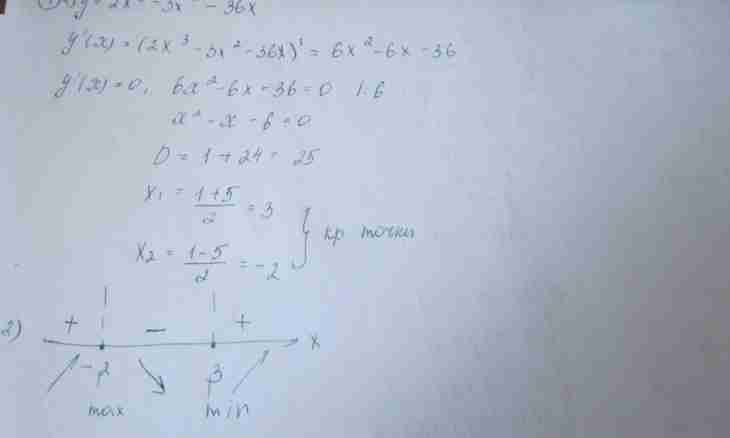By definition, M0 point (x0, y0) is called a point of a local maximum (minimum) of function of two z=f variables (x, y) if in some vicinity of a point of U (x0, y0), for any point of M (x, y) f (x, is executed by yf (x0, y0)). These points are called function extrema. In the text the private derivatives are designated according to fig. 1.
Instruction
1. A necessary condition of an extremum is equality to zero private derivatives of function on x and on y. M0 point (x0, y0) in which in zero both private derivatives address, is called a stationary point of the z=f function (x, y).
2. Remark. The private derivative z=f functions (x, y) can not exist in an extremum point therefore points of a possible extremum are not only stationary points, but also points in which private derivatives do not exist (to them there correspond surface edges – a function graph).
3. Now it is possible to pass to sufficient conditions of existence of an extremum. If differentiable function has an extremum, then it can be only in a stationary point. Sufficient conditions of an extremum are formulated as follows: let in some vicinity of a stationary point (x0, y0) function f (x, y) has continuous private derivatives of the second order. For example: (cm. fig. 2)
4. Then: a) if Q> 0, then in a point (x0, y0) function has an extremum, and at f’’ (x0, y0) 0) - a local minimum; b) if Q
5. For search of an extremum of function of two variables it is possible to offer the following scheme: at first there are stationary points of function. Then in these points sufficient conditions of an extremum are checked. If function in any points has no private derivatives, then in these points there can be an extremum too, but sufficient conditions will not be applicable any more.
6. Example. To find z=x^3+y^3-xy function extrema. Decision. Let's find stationary points of function (see fig. 3):
7. The solution of the last system gives stationary points (0, 0) and (1/3, 1/3). Now it is necessary to check performance of a sufficient condition of an extremum. Find the second derivatives and also stationary points of Q(0.0) and Q (1/3, 1/3) (see rice 4):
8. As Q(0, 0)0, therefore, in a point (1/3, 1/3) an extremum is. Taking into account that the second derivative (on xx) in (1/3, 1/3) more than zero, it is necessary to make the decision that this point is a minimum.